The Importance of Precision in Statistics
Statistics play a crucial role in various fields, from scientific research to business decision-making. One key aspect that cannot be overlooked in statistical analysis is precision.
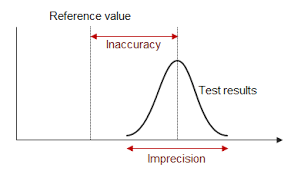
Precision in statistics refers to the degree of exactness or accuracy in the measurements and calculations used to describe data. It is essential for drawing reliable conclusions and making informed decisions based on the data at hand.
When conducting statistical analysis, precision ensures that the results are consistent and reproducible. It helps researchers and analysts avoid errors and misinterpretations that could lead to flawed conclusions.
Measures of central tendency, such as mean, median, and mode, rely on precise calculations to accurately represent the data distribution. Similarly, measures of dispersion, like standard deviation and variance, provide insights into the spread of data points around the central value.
Statistical inference, hypothesis testing, and confidence intervals all require precise calculations to assess the significance of results and make valid predictions about populations based on sample data.
Moreover, precision is crucial when dealing with large datasets or complex statistical models. Even small errors or inaccuracies in calculations can have significant implications for the outcomes of analyses.
In summary, precision in statistics is not just a desirable quality but a fundamental requirement for meaningful data analysis. By ensuring accuracy and exactness in measurements and computations, statisticians can provide reliable insights and support informed decision-making across various disciplines.
Understanding Precision in Statistics: Key Questions Answered
- What is precision in statistics?
- What is precision in statistics example?
- What is precision defined as?
- How is precision measured in statistics?
What is precision in statistics?
Precision in statistics refers to the level of exactness and accuracy in the measurements and calculations used to describe data. It is a critical concept that ensures the reliability and consistency of statistical analysis. In statistical terms, precision is about how close individual measurements or values are to each other when repeated under the same conditions. A high level of precision indicates that the results are consistent and reproducible, reducing the likelihood of errors or misinterpretations in drawing conclusions from the data. Understanding and maintaining precision in statistical analysis is essential for making informed decisions based on reliable data.
What is precision in statistics example?
Precision in statistics refers to the level of exactness and consistency in measurements and calculations used to describe data. An example of precision in statistics can be seen in the measurement of a pharmaceutical product’s dosage. If a medication needs to be administered in precise amounts to ensure its effectiveness and safety, statistical analysis can help determine the exact dosage required based on rigorous measurements and calculations. Precision ensures that the dosage is accurately determined and maintained within a specific range to achieve the desired therapeutic outcome without risking potential harm to patients.
What is precision defined as?
Precision in statistics is defined as the degree of exactness or accuracy in the measurements and calculations used to describe data. It refers to the ability to consistently obtain similar results when measurements are repeated. In statistical analysis, precision is crucial for ensuring reliable and reproducible outcomes, as well as for drawing accurate conclusions based on the data at hand. A high level of precision indicates that the results are closely clustered around a central value, providing a clear and consistent representation of the underlying data distribution.
How is precision measured in statistics?
In statistics, precision is commonly measured through metrics such as standard deviation, variance, and confidence intervals. Standard deviation quantifies the dispersion of data points around the mean, indicating how closely grouped the values are. A smaller standard deviation implies higher precision, as data points are closer to the average. Variance is another measure of spread that complements standard deviation by providing a numerical value for the variability within a dataset. Confidence intervals indicate the range within which a population parameter is likely to fall, offering insights into the precision of estimates derived from sample data. These statistical measures help assess and communicate the level of precision in data analysis and decision-making processes.